三角形の比に関する定理のうちの、高校の数学で学習する「メネラウスの定理」(Menelaus' theorem)と、「チェバの定理」(Ceva's theorem)について、以下に内容をまとめておく。
　この定理について解説している諸々の参考書の説明には、分りにくいものが多い。よって、ここに分りやすい理解の仕方を示すことにする。

メネラウスの定理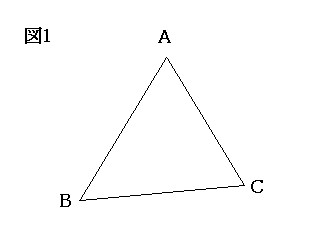


　図１のような三角形ＡＢＣにおいて、いずれの頂点をも通らない一本の直線を引く。このとき、その直線が三角形の３辺もしくはその延長線のいずれとも交わるようにし、その直線と線分ＢＣもしくはその延長線との交点をＰ、ＣＡもしくはその延長線との交点をＱ、ＡＢもしくはその延長線との交点をＲとする。(図2)

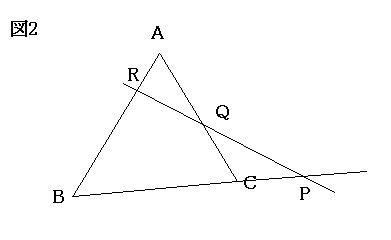
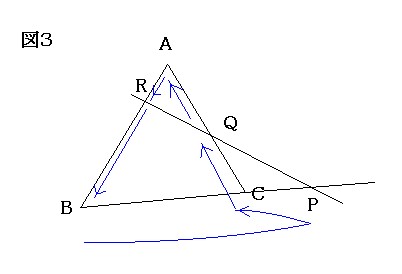
このとき、下図３のように

と表される。
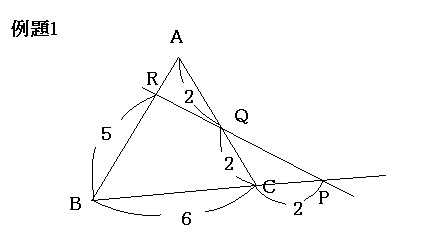
　例題１において、ＡＲの長さを求めてみよう。

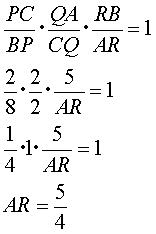
チェバの定理


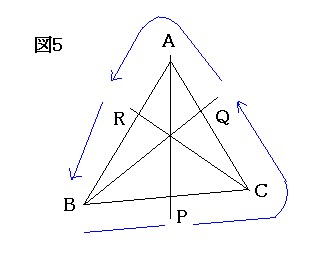
　図１のような三角形ＡＢＣにおいて、それぞれの頂点から、対辺もしくはその延長線上にそれぞれ一本の直線を引く。このとき、その３直線が一点で交わるようにし、点Ａを通る直線と線分ＢＣ(もしくはその延長線)との交点をＰ、 点Ｂを通る直線と線分ＣＡ(もしくはその延長線)との交点をＱ、点Ｃを通る直線と線分ＡＢ(もしくはその延長線)との交点をＲとする。(図4)

このときも、下図５のように

と表される。
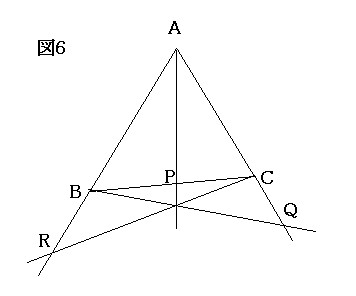
　下図６の場合にも、この関係は成り立つ。

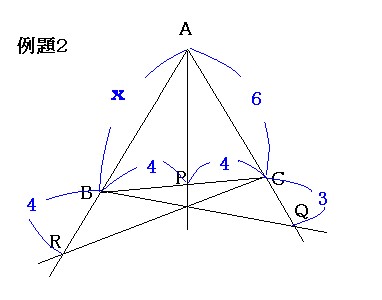
　例題２において、ＡＲの長さを求めてみよう。

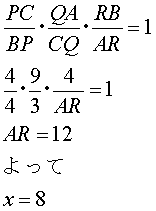
　通常の形では、どちらの定理もくるり一回転させるのがコツです。