「等差数列」(arithmetic sequence)について、以下に内容をまとめておく。

等差数列……等間隔で増加(または減少)する数列

「初項」(first term)……数列の最初の項
　a1 または単に ａ と表す

「末項」(last term)……数列の最後の項
　ｌ (小文字のエル)で表す

「公差」(common difference)……数字と数字の間隔
　d と表す。年齢の場合には公差は１、奇数の列の場合には公差は２である。

等差数列の一般項
　ｎ番目の数を表す an は、次の一般式(公式化した式)に当てはめれば求められる。

　１から始まる正の奇数の列の15番目の数字は何であるかを考える。この場合には、この便利な公式がある。すなわち、１から始まる正の奇数の列の15番目の数字は、

になる。

等差数列の和
　初項から n 番目の数までの和を表す Sn は、次の一般式(公式化した式)に当てはめれば求められる。

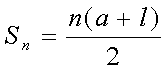
　初項と末項をたして、それに項数を掛け、さらにその全体を２で割ればよい。例えば、５から21まで(５と21を含む)の奇数の和は、この間に奇数は5, ７, 11, 13, 15, 17, 19, 21の８つの項があるから、


自然数の和(１からnまでの)
　自然数とは、１から始まる公差１の数列である。２番目の項は２、３番目の項は３、n番目の項はnである。つまり、末項は項数と同じnである。また、初項は１である。であるから、この数列の和 Sn は、

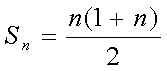
という一般式で表される。

奇数の和
　さらに、１から始まる正の奇数の(ｎ番目の数までの)和は、１番目の項が１、２番目の項が (2×2-1)=3、３番目の項が (2×3-1)=5、ｎ番目の項が (2n-1)になるから、その一般式は、

という一般式で表される。
　同様に、-１から始まる負の奇数の(n番目の数までの)和は、

と表される。