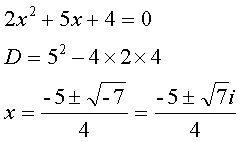２次方程式の解き方

平方根の考え方を利用する解き方

  
という形になる方程式を２次方程式(quadratic equation)という。

  この等式において、b = 0 (a≠0) になるときは、
  
という簡単な数式に変化する。

例
                   

……………………………………

因数分解を利用する解き方

  
という形の方程式において、
  
の部分を因数分解できるときには、簡単に解を求めることができる。

例
                   

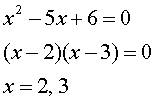
 ※因数のどちらか一方がゼロになれば、この等式は成立する。

……………………………………

解の公式を利用する解き方

  
という形の式においては、
  
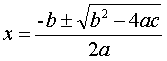
という一般式を用いた解法が成立する。

例
  

……………………………………

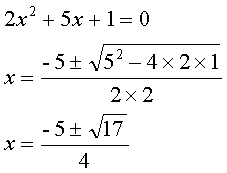
解を判別する

  ２次方程式の解は、原則として２つ求められる。しかし、解が重なって１つになったり(重解)、あるいは実数の範囲では解がなくなったりする場合もある。

実数の解が２つ求められる場合

  上の実例で示したように、解の公式を用いて２次方程式を解く場合に √の中の
b×b - 4×a×c の部分が正の数 になるとき、実数の解が２つ求められる。

  
の解を求める式

  
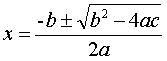
において

  
として、

D > 0
のとき、実数解が２つ求まる。

例
  

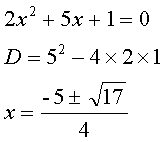
実数の解が１つだけ求められる場合

D = 0
のとき、実数解が１つ求まる。

例
  

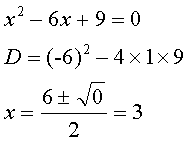
実数の解が求められない場合

D < 0
のときには実数の解は求められないが、虚数の解が２つ求まる。

例