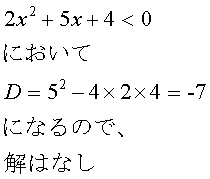�Q���s�����̉�����
�������̍l�����𗘗p���������
![]()
��������
![]()
�Ƃ����`�ɂȂ���������Q�s����(quadratic inequality)�Ƃ����B
���̓����ɂ����āAb = 0 (a��0) �ɂȂ�Ƃ��́A
![]()
��������
![]()
�Ƃ����ȒP�Ȑ����ɕω�����B
��

![]()

�c�c�c�c�c�c�c�c�c�c�c�c�c�c
���������𗘗p���������
![]()
��������
![]()
�Ƃ����`�̕������ɂ����āA
![]()
�̕��������������ł���Ƃ��ɂ́A�ȒP�ɉ������߂邱�Ƃ��ł���B
��
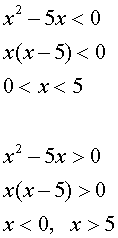
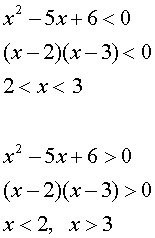
�����̂ǂ��炩�P���[���ɂȂ�A���̓����͐�������B
��Ȃ͕̂s�����̌����ł���A�Ⴆ�����̎��ɂ����� x = 1 �� x = 4 �̂Ƃ��ɂ͍��ӂ��v�Z����ƕ��̐��ɂȂ�Ax = -1 �� x = 6 �̂Ƃ��ɂ͍��ӂ��v�Z����Ɛ��̐��ɂȂ�B
�c�c�c�c�c�c�c�c�c�c�c�c�c�c
���̌����𗘗p���������
![]()
�Ƃ����`�̕������ɂ����ẮA
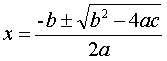
�Ƃ�����ʎ���p������@����������B
���̂Ƃ��ɋ��߂���Q�̉��� �� , �� �Ƃ���B(�����ł́A�������ق��̉��� �� , �傫���ق��̉��� �� �Ƃ���)
�s�����̏ꍇ�ɂ́A�s�����̌����ƁA��̒���
���@���̐��ɂȂ邩�A�A�[���ɂȂ邩�A�B���̐��ɂȂ邩�ɂ���āA�قȂ������ʂ�B
�c�c�c�c�c�c�c�c�c�c�c�c�c�c
![]()
�Ƃ��āA
�@�c �����̐��ɂȂ�ꍇ
���ʎ������̐��ɂȂ�ꍇ
(1)
![]()
�̂Ƃ��ɂ�
![]()
(2)
![]()
�̂Ƃ��ɂ�
![]()
��


�A�c �� 0 �ɂȂ�ꍇ
���ʎ����[���ɂȂ�ꍇ
(1)
![]()
�̂Ƃ��ɂ�
![]()
�Q���������̉����d���ɂȂ� �c = 0 �̏ꍇ�ɂ́A (x-��) ���Q�悵�ĕ��ɂȂ���͂Ȃ��B
(2)
�Q���������̉����d���ɂȂ�ꍇ�ɂ́A���� = �E�� = 0 ���[�������������P���܂�B
���������āA
![]()
�̂Ƃ��ɂ�
���́A���ȊO�̂��ׂĂ̎���
![]()
�̂Ƃ��ɂ�
���͂��ׂĂ̎���
��
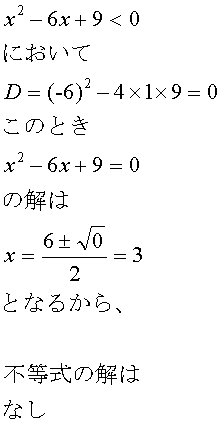
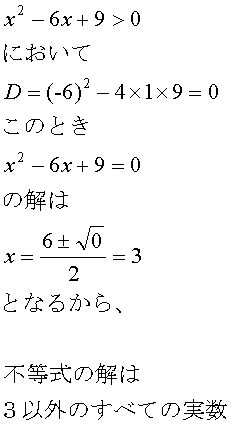
�B�c �����̐��ɂȂ�ꍇ
���ʎ������̐��ɂȂ�ꍇ
(1)
![]()
�̂Ƃ��ɂ�
![]()
�ؖ��͊������邪�A���̏ꍇ�̉��͑��݂��Ȃ��B
(2)�̂Ƃ��ɂ�
���͂��ׂĂ̎���
�����
![]()
����������A
![]()
�������I�ɐ������邩��A
���̏ꍇ�ɂ�
���͂��ׂĂ̎���
��