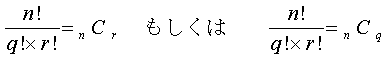Ｐ
					Ｑ

  右の図のように、東西に４本、南北に５本の道路がある。このとき、Ｐ地点からＱ地点まで、遠回りをしないで行く道順は何通りあるか。

Ｐ	→	→	→	→
					↓
					↓
					↓
					Ｑ

  遠回りをしないで行く道順は、右図のように右へ４区画、下へ３区画歩けばよいことになる。
  ところで、右へ４区画と下３区画の順番は、どのような順番でもよいことになる。すなわち、→ →↓→ →↓↓でもよいし、↓↓↓→ → → → でもよい等々である。

  それでは、これを数式化して道順の数を求めるためには、どのような考え方をすればよいのであろうか。
  一番分かりやすいのは、次のように考えることである。まず便宜上１本の横道を進むと考える。すなわち、→ → → → → →  → のように進むと考える。次に、この中のどこか３箇所で下へ１区画進むと考える。すなわち、→ →↓→↓↓→ や、↓→ →↓→ →↓のように。

  これは、一郎から七郎までの７人を一列に並べて、その中で誰か３人↓へ進む者を選ぶ場合と同じであるから、その数式は
  
である。一般化すると、進む区画の総数をn、下へ進む回数をrとすれば、
  
となる。
  この式を別の公式 (同じものを含む順列) から導くことも可能である。すなわち、

  

  

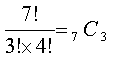
  一般化すれば、進む区画の総数をn、東へ進む回数をq、下へ進む回数をrとすると、