高校の数学では、「ベクトル」(vector)という項目を学習する。数学では高校で初めて登場するのであるが、実は中学の理科の時間にその基礎を学習している。
力の合成
  
|
|
ベクトルの加法
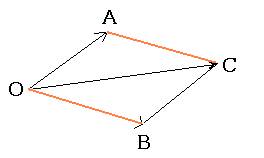  
|
|
ベクトルの減法
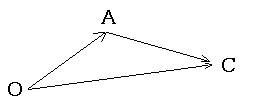 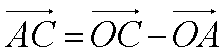 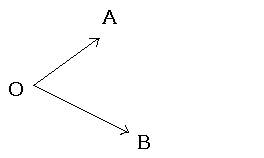 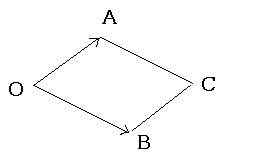 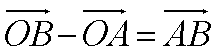
|
|