高校数学には、「数列 sequence」(現在は数Bで学習)という学習項目がある。高校数学の数列の学習では比較的簡単な内容から、「漸化式」(recursive formula)、「数学的帰納法」(mathematical induction)など難易度の高い内容まで順次進んで行く。
ところで、そもそも「数列」とは何であろうか? どのような意味をもっているのであろうか? この素朴な問い掛けなしには、「数列」への興味は沸いてこないと思われる。
日常生活の中でも、数列は随所に登場する。例えば、銀行のカードの4桁の暗証番号は、立派な数列である。この場合には、0000から9999まで、10×10×10×10 = 10000とおりの数列が存在することになる。数列にはこの例のような「有限数列」(finite sequence)と、円周率のような「無限数列」(infinite sequence)とが存在する。
数列では「初項」(first term)をa1または単にaで表し、「末項」(last term)をl (小文字のエル)で表す。さらには、その数列にいくつの数が存在するかを示す「項数」(number of terms)をnで表す。
銀行のカードに4桁の整数を記憶させる場合には、例えば、初項は7、次の項は3、次の項は9、末項は1といったように不規則な数列になっている。このような数列を「乱数列」(Random number sequence)という。高校の数学で学習するのは、このような乱数列ではなく、規則的な数の並び方のある数列である。
規則的な数列の中で最も我々に身近なものは、人生の数列(年齢)である。我々の年齢は、この世に生れ落ちたときを 0 とし、1年後の誕生日には1に、2年後の誕生日には2になる。であるから、「初項」は 0 である。また、毎年1歳ずつ増えて行くという規則をもった数列である。このように等間隔で増加(または減少)する数列を「等差数列」(arithmetic sequence)という。そして、数字と数字の間隔を「公差」(common difference)といい、dで表す。年齢の場合には公差は1、奇数の列の場合には公差は2である。
いま、1から始まる正の奇数の列の15番目の数字は何であるかを考える。この場合には便利な公式がある。n番目の数を表すan は、次の一般式(公式化した式)で求められる。すなわち、
![]()
1から始まる正の奇数の列の15番目の数字は
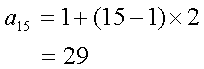
になる。